有大半年没有打开简书了(愧对各位默默关注我的读者),得空看了下简书后台的评论,整理了下发现很多新入坑的伙伴的主要问题还是针对绘图和数据处理的(比如很多小伙伴不知道自己要画什么图,或者知道自己要画什么但是不知道怎么把手中的数据变成需要的图),这里就一并合在一起谈谈我对数据处理和绘图思路的理解(主要是思路),若有不妥还请指正。主要是针对新入门的。
把绘图说的正式一点,就是数据可视化,其本质还是对于数据的呈现方式,所以所有的图片本身不过还是数据而已。对于计算机来说就是二维的像素矩阵,每个像素有自己的颜色,所以呈现出了一张平面图片。对于我们要做的气象绘图而言,也不过是把形式不同的数据变成最终想要的图片。所以在绘图前应该是首先确定自己要呈现怎样的效果,为了这个效果来制定符合的图片类型,然后再分析这种图片类型是由什么格式的数据实现的,最后再去寻找响应的数据并处理。实际上这是一个逆向的思维过程,那我们先从简单的折线图开始。
比如说我们在文献中看到了类似图1-折线图1,需要模仿绘制。那么首先观察这幅图的特征,其本质就是200个点连起来的折线,所以这幅图的本质就是200个点构成的序列,假设这幅图是近200年的区域平均降水量,而我们手中的数据是(年,月,经度,纬度)的降水量数据,那么我们对月平均和经度,纬度这三个纬度进行平均,就可以得到数据格式为(年)的序列。之后利用绘制折线图的函数ax.plot(x,y)就可以了(如果是温度廓线,那么对应的x就是温度,y就是高度;如果是某变量如阻塞指数沿经度分布,那么y就是阻塞指数,x就是经度,灵活应用即可)。
那么现在把折线图变得复杂一些:
这种图常见于预估类的文献,阴影区间表示浮动范围(假如是正负一倍标准差), 那么我们需要计算的就是中间的序列,以及它的浮动范围,本质上依然是三条折线(折线本身+(折线+1δ)+(折线-1δ))。如果不知道绘制阴影的函数,将其绘制成三条折线的效果也是一样的,浮动范围可以用虚线。如果想要绘制阴影,百度下”matplotlib如何绘制阴影区间”也可以搜到plt.fill_between这个函数。把图换成柱状图本质也是一样的(一条序列)。
提到预估类的工作就不得不提到箱线图(主要用来分析和对比数据分布情况的,分布情况主要指的是离散程度,分位数位置等等),这里就献丑以我自己的一个工作来展示。
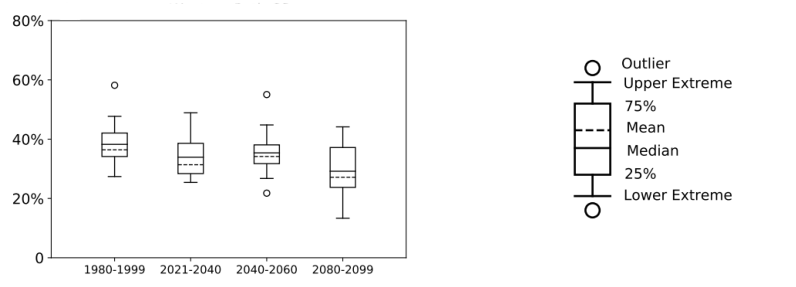
我这里是对比了四个时间区段的情况,图例清楚的说明了箱体和箱须分别代表的含义。那么需要怎样的数据来实现这幅图呢?首先可以确定的这是四组数据(肯定是四组由数字构成的一维数组),对于python来说,不需要我们事先计算每组数据的均值,中位数,分位数等等,只需将原始数据放入绘图函数ax.boxplot即可。所以我们只在指定的X轴的对应位置使用四次ax.boxplot函数。
接下来再说说等值线图:

不要看它是N条线组成的就以为它的组成数组是N个序列!高中地理就都学过等高面图,就是把相等大小的点连在一起。所以可以看到图4-等值线图1每条线的颜色是不一样的,因为颜色是反应组成这条线的数的大小。所以实际上这幅图是由N*M个点组成的,每个点都有一个数字,把大小相同的数字连接起来构成等值线图(等下用填色图更好理解)。所以这张图需要一个(N,M)的数组通过ax.contour函数实现。这个(N,M)数组的获取方式,需要分析N是什么,M是什么。如果是空间分布,那就是将原数据保留经纬度,将其它维度(时间,高度)处理,如果是纬高分布,那就将纬度和高度保留,同理,如果是纬度-时间分布,就保留纬度和时间。

现在将空白区域进行了填色,处于两条等值线之间的区域为同一颜色。也就是说,处于同一个区间范围的,为同一种颜色。
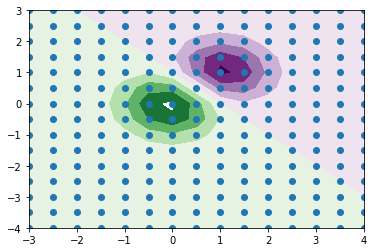
我进一步对每一个点进行了标记来方便理解。这幅图就是由这么多个点的同样形状的(N,M)数组构成,每个点都有自己的大小(也就对应了其颜色)。
再进一步的,我们通常要进行显著性检验,也就是对填色图进行一个”打点”的操作。让过检部分加上阴影或者dots。实现思路是这样的:打点或者添加阴影本质也是一种填色,只不过填的不是颜色,而是一种特殊的标记。所以我们只需要在过检部分填色就好了,设置方法是通过ax.contourf函数的level参数设置填色区间,用hatches参数设置填色标记,我们在进行检验计算时,都会返回对应的P值数组,P<0.05为通过0.05显著性检验,所以这时只需对P值数组0-0.05范围进行标记填充即可。
再来说说矢量绘制:

我们首先要知道,矢量的构成,要表达矢量,需要有两个要素,也就是大小和方向,通过正交分解则变成了i矢量和j矢量。对于风场来说,就是u,v。对于上边的前边的填色图来说,是由(N,M)的数组构成,颜色反应每个点的数值。那对于矢量场来说,依然是(N,M)的数组组成的,箭头反应每个点的矢量,特殊的在于,需要同时使用u,和v才能正确表达矢量。所以本质应该是u(N,M)和v(N,M)的叠加。所以绘制时只需要对ax.quiver()函数同时输入u,v即可。
对于散点图而言,它就像缺失了很多数据的填色图一样(或者理解为仅保留了部分点的填色图),所以它一定不是(N,M)数组构成的了。要绘制填色图,我们首先要知道每个点的x和y的位置,其次也要知道这个点的大小(反应为颜色),所以它是由(n,3)组成的,n指n个点,3分别为x,y和点本身的大小。
总的来说,先根据自己需要画的图来设计目标数据(比如我要画折线图,那我就需要1条序列;我需要填色图,我就需要1个(N,M)数组),确定自己目标数据的形状,然后再根据目标数据的形状来处理原始数据。同样的,在模仿一幅图的时候,先确定它的数据形状,再根据它的X,Y轴确定它图形背后数组的实际意义,才能有针对性的获取和处理数据。至于其它细节性的修饰,如何让图更美观,就考验后期的调整了。当然matplotlib官方本身已经提供了大量的示例,几乎包含了常规图形,不妨收藏在书签栏,画图前看看有没有类似自己需要的,直接拿来修改当然是最方便的。最后一定要善于利用度娘,搜索matoplotlib如何绘制xxxxx,或者python如何让折线图更美观等等。