曼-肯德尔(Mann-Kendall)检验

Function 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
'''
曼-肯德尔(Mann-Kendall)检验
输入：
inputdata：输入数据，一维序列
输出：UF,UB
'''
def mktest(inputdata):
    inputdata = np.array(inputdata)
    n=inputdata.shape[0]
    Sk             = [0]
    UFk            = [0]
    s              =  0
    Exp_value      = [0]
    Var_value      = [0]
    for i in range(1,n):
        for j in range(i):
            if inputdata[i] > inputdata[j]:
                s = s+1
            else:
                s = s+0
        Sk.append(s)
        Exp_value.append((i+1)*(i+2)/4 )                    
        Var_value.append((i+1)*i*(2*(i+1)+5)/72 )            
        UFk.append((Sk[i]-Exp_value[i])/np.sqrt(Var_value[i]))
    Sk2             = [0]
    UBk             = [0]
    UBk2            = [0]
    s2              =  0
    Exp_value2      = [0]
    Var_value2      = [0]
    inputdataT = list(reversed(inputdata))
    for i in range(1,n):
        for j in range(i):
            if inputdataT[i] > inputdataT[j]:
                s2 = s2+1
            else:
                s2 = s2+0
        Sk2.append(s2)
        Exp_value2.append((i+1)*(i+2)/4 )                    
        Var_value2.append((i+1)*i*(2*(i+1)+5)/72 )            
        UBk.append((Sk2[i]-Exp_value2[i])/np.sqrt(Var_value2[i]))
        UBk2.append(-UBk[i])
    UBkT = list(reversed(UBk2))
    return UFk, UBkT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from scipy import signal
import numpy as np

y = np.array([15.4,14.6,15.8,14.8,15.0,15.1,15.1,15.0,15.2,15.4,
              14.8,15.0,15.1,14.7,16.0,15.7,15.4,14.5,15.1,15.3,
              15.5,15.1,15.6,15.1,15.1,14.9,15.5,15.3,15.3,15.4,
              15.7,15.2,15.5,15.5,15.6,15.1,15.1,16.0,16.0,16.8,
              16.2,16.2,16.0,15.6,15.9,16.2,16.7,15.8,16.2,15.9,
              15.8,15.5,15.9,16.8,15.5,15.8,15.0,14.9,15.3,16.0,
              16.1,16.5,15.5,15.6,16.1,15.6,16.0,15.4,15.5,15.2,
              15.4,15.6,15.1,15.8,15.5,16.0,15.2,15.8,16.2,16.2,
              15.2,15.7,16.0,16.0,15.7,15.9,15.7,16.7,15.3,16.1])

uf,uk = mktest(y)

fig = plt.figure(figsize=(15,15))
f_ax1 = fig.add_axes([0.1, 0.1, 0.4, 0.3])
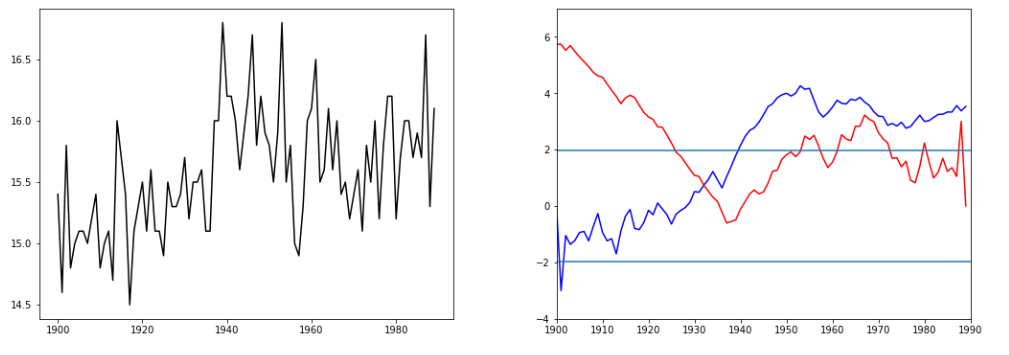
f_ax1.plot(np.arange(1900,1990,1),y,'k')

f_ax2 = fig.add_axes([0.6, 0.1, 0.4, 0.3])
f_ax2.plot(np.arange(1900,1990,1),uf,'b',label='UF')
f_ax2.plot(np.arange(1900,1990,1),uk,'r',label='UK')
f_ax2.set_xlim(1900,1990)
f_ax2.set_ylim(-4,7)
# 0.01显著性检验
f_ax2.axhline(1.96)
f_ax2.axhline(-1.96)
plt.show()

image-20200521090912932