滑动平均

Function

滑动平均是趋势拟合的基础方法，也相当于一个滤波器，比如使用九点滑动平均来分析时间序列的年代际变化。 python的常用算法库中并未给出直接计算滑动平均的函数。但是numpy库中给出了一个更加强大更加基础的函数，卷积numpy.convolve()。

1
numpy.convolve(a, v, mode='full')

参数：

　　　　a:(N,)一维数组

　　　　v:(M,)一维数组

　　　　mode:{‘full’, ‘valid’, ‘same’}参数可选

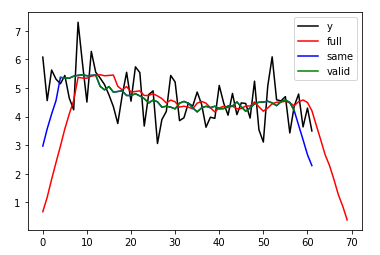
　　　　　　‘full’　默认值，返回每一个卷积值，长度是N+M-1,在卷积的边缘处，信号不重叠，存在边际效应。

　　　　　　‘same’　返回的数组长度为max(M, N),存在边际效应。

　　　　　　‘valid’ 　返回的数组长度为max(M,N)-min(M,N)+1,此时返回的是完全重叠的点。无边际效应。

通俗地讲，a是原始序列，v是卷积核。将上述函数转化为滑动平均的原理，就是设置一个等权重的卷积核，对原始序列进行卷积运算即可。实际上，卷积运算就是滑动平均的推广。

1
2
def np_move_avg(a,n,mode):
    return(np.convolve(a, np.repeat(1/n, n), mode=mode))

参数：

　　　　a:(N,)一维数组

　　　　n:int型整数，n=9即为9点滑动平均

　　　　mode 等同numpy.convolve()中的参数mode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import matplotlib.pyplot as plt
def np_move_avg(a,n,mode):
    return(np.convolve(a, np.repeat(1/n, n), mode=mode))

y = np.array([6.08, 4.56, 5.63, 5.31, 5.15, 5.44, 4.65, 4.24, 7.3,  5.86, 4.51, 6.28, 5.55, 5.35,
              5.12, 4.76, 4.35, 3.76, 4.74, 5.55, 4.54, 5.74, 5.54, 3.67, 4.77, 4.9,  3.06, 3.9,
              4.18, 5.44, 5.21, 3.86, 3.96, 4.47, 4.37, 4.86, 4.43, 3.63, 3.98, 3.94, 5.09, 4.48,
              4.05, 4.81, 4.07, 4.48, 4.46, 3.95, 5.24, 3.54, 3.11, 5.07, 6.09, 4.59, 4.55, 4.7,
              3.43, 4.37, 4.79, 3.64, 4.3,  3.5 ])
y_smooth9_full = np_move_avg(y,9,'full')
y_smooth9_same = np_move_avg(y,9,'same')
y_smooth9_valid = np_move_avg(y,9,'valid')

plt.plot(np.arange(0,62,1),y,'k',label='y')
plt.plot(np.arange(0,62+8,1),y_smooth9_full,'r',label='full')
plt.plot(np.arange(0,62,1),y_smooth9_same,'b',label='same')
plt.plot(np.arange(0+4,62-4,1),y_smooth9_valid,'g',label='valid')
plt.legend()

image-20200519214305477