线性倾向估计(一元线性回归)

Function

除1.132节介绍的的线性回归系数可用来计算线性回归外，sklearn库中也有相关的函数用来计算一元线性回归，同时还可以输出回归线，为数据可视化提供了便利。

1
2
from sklearn.linear_model import LinearRegression
LinearRegression(fit_intercept=True, normalize=False, copy_X=True)

参数：

fit_intercept ：是否计算截距，若数据已中心化，则可以不计算。默认True。

normalize ：若开启，则对数据进行归一化处理。

copy_X ：若开启，则复制X，否则对X进行重写覆盖。

属性：

coef_ ：线性回归系数

intercept_ : 截距

方法：

fit(x,y) ：建立x,y的回归模型

predict(x) ：利用回归模型进行预测

score(x, y[, sample_weight]) ：返回R^2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
#建立数据
x = np.arange(2000,2011,1).reshape(-1, 1)
y = np.array([3.9, 4.4, 10.8, 10.3, 11.2, 13.1, 14.1,  9.9, 13.9, 15.1, 12.5]).reshape(-1,1)
#创建回归模型
solver = LinearRegression()
#对x,y进行回归计算
solver.fit(x,y)
#计算x对应的回归值
regressline = solver.predict(x)
#绘图
plt.scatter(x,y)
plt.plot(x, regressline, color='k',linewidth=3)
plt.show()

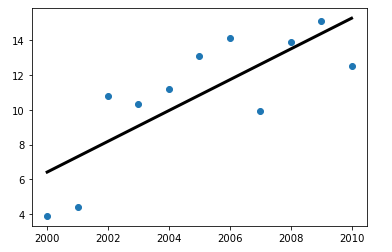
image-20200519214110927

该方法较1.132节相对繁琐，甚至有些小题大做。因为该方法主要用于通过已有数据建立回归模型，对未知数据进行一元回归预测，在机器学习中使用更为广泛，在此处，仅仅体现了较为方便的回归线的绘制。